线段树入门

蒟蒻刚学完线段树不久，写一篇线段树入门笔记。

线段树是一种二叉搜索树，是 $OI$ 中很重要的数据结构。其支持单点修改，区间修改，单点查询，区间查询（最大最小值、求和）等操作。虽然比树状数组慢，但是它支持的操作更多。

线段树可以高效地解决具有区间性质的问题，例如区间求和，一次操作(修改，查询)就要遍历整个数组，单次操作时间复杂度 $O(n)$ ，$q$ 次修改复杂度 $O(nq)$ ，远远超时。而线段树单次修改时间复杂度 $O(\log n)$ ， $q$ 次修改复杂度 $O(q \log n)$ ，节约的不少时间。

线段树基本结构

比如一个长度为 $5$ 的集合 $\{8,3,11,4,13\}$ ，要维护他它的区间总和，建造出的线段树如下图所示：

如图所示，线段树的性质如下：

• $1.$ 线段树的每一个节点都管理着一段区间，其值为这一区间内需要维护的值，根节点（编号为 $1$ ）管理着整段区间 $[1,n]$ ，叶子节点管理的区间长度为 $1$ 。

• $2.$ 除叶子节点外，其他节点分别有两个子节点，如当前节点的编号为 $p$ ,则左子节点的编号为 $2p$ ，右子节点的编号为 $2p+1$ 。

• $3.$ 如节点 $p$ 的管理区间为 $[l,r]$ ，设此区间的中点为 $mid$ ，则左子节点管理区间的范围是 $[l,mid]$ ，右子节点管理区间的范围是 $[mid+1,r]$ 。

线段树建树

这里以维护区间总和为例子。

我们考虑每个节点需要储存的信息有：当前节点管理区间的左右端点，维护的值，以及标记等(后面会讲到)，我们可以用一个结构体存储。

代码：

struct Node{
    int l,r; //左右端点
    long long sum; //维护总和
}tree[4*n];

线段树空间一定要开原数组的4倍，不然很有可能爆空间。

因为树具有天然的递归性质，所以我们可以用递归建树。如果当前节点是叶子节点，那么将其赋值为当前区间的值，否则递归build一下左子树，再build一下右子树，最后回传一下左右子节点的 $sum$ 就可以了。

代码：

//p为当前节点编号，l为当前区间起点，r为当前区间终点
void build(int p,int l,int r){
    tree[p].l=l,tree[p].r=r; //当前树的管理区间范围
    if(l==r){
        tree[p].sum=a[l]; //叶子节点直接赋值
        return;
    }
    int mid=(l+r)/2; //区间中点
    build(p*2,l,mid); //递归建左子树
    build(p*2+1,mid+1,r); //递归建右子树
    pushup(p); //回传sum
}

回传pushup的时候，对于区间性质的问题来说，就是将左右两个节点的答案合并就可以了。

示例图：

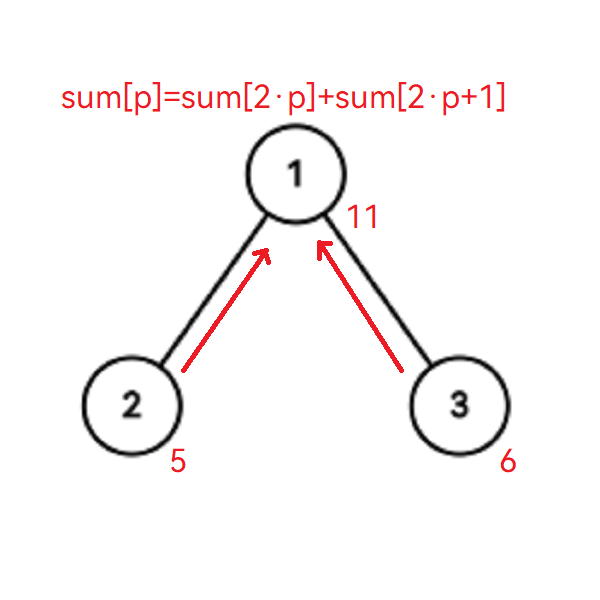
区间求和公式如下：

$sum_{p}=sum_{2p}+sum_{2p+1}$

区间最大/最小值公式如下：

$sum_{p}=\max(sum_{2p},sum_{2p+1})$

代码：

//p为当前节点编号
void pushup(int p){
    tree[p].sum=tree[p*2].sum+tree[p*2+1].sum;
}

建树时间复杂度可以估计为 $O(n)$ ，因为需要遍历所有的节点。

线段树单点修改

比如要将$a_x$ 的数值修改，就是将线段树中区间起点为 $x$ 且长度为 $1$ 的节点修改，然后再回传回根节点，那么整体的思路如下：

• $1.$ 从根节点出发，往下寻找目标节点，修改其值。

• $2.$ 将总和回传到根节点。

举个例子，还是之前的集合 $\{8,3,11,4,13\}$ ，现要将第 $2$ 个数 $3$ 加上 $6$ ，操作如下图所示：

我们可以考虑使用递归实现。如果是目标节点，那么修改，然后return，否则递归向下，目标在左边就遍历左子树，目标在右边就遍历右子树，最后回传总和就可以了。

代码：

//p为当前节点编号，x为要修改的位置，k为要加上的值
void update(int p,int x,int k){
    if(tree[p].l==tree[p].r){ //要修改的节点
        tree[p].sum+=k; //直接修改，返回
        return;
    }
    int mid=(tree[p].l+tree[p].r)/2;
    if(x<=mid)update(p*2,x,k); //在左子树，递归到左边
    if(x>mid)update(p*2+1,x,k); //在右子树，递归到右边
    pushup(p); //回传sum
}

单点修改的时间复杂度为 $O(\log n)$ ，因为向下递归到叶子节点是遍历树的深度。

线段树区间查询

单点查询没什么可说的吧，和单点修改类似，我们主要看一下区间查询。

区间查询分为三种情况：

• $1.$ 当前节点的区间包含在查询区间之内，直接返回当前节点的 $sum$ 值。
• $2.$ 当前区间与左子树区间有重叠部分，那么递归搜索左子树，加上答案。
• $3.$ 当前区间右子树区间有重叠部分，那么递归搜索右子树，加上答案。

还是之前那个例子，比如查询区间 $[2,4]$ ，如下图所示：

一般来说查询要加long long，因为所有数的总和有可能爆int。

代码：

//p为当前节点编号，l为查询区间的左端点，r为查询区间的右端点
long long query(int p,int l,int r){
    if(tree[p].l>=l&&tree[p].r<=r){ //在查询区间内
        return tree[p].sum; //直接返回值
    }
    long long ans=0;
    int mid=(tree[p].l+tree[p].r)/2;
    if(l<=mid)ans+=query(p*2,l,r); //如果左子树区间有重叠部分，答案加上左边的查询
    if(r>mid)ans+=query(p*2+1,l,r); ////如果右子树区间有重叠部分，答案加上右边的查询
    return ans;
}

区间的时间复杂度为 $O(\log n)$ ，因为每次查询都要将线段树一分为二，最后会分成 $\log n$ 个部分。

P3374 【模板】树状数组 1

虽然此题的题目看起来和线段树毫不相干，但是这可以用线段树去做。

这是一个线段树单点修改，区间查询的模板题。

代码：

#include<bits/stdc++.h>
using namespace std;
struct Node{
    int l,r; //左右端点
    long long sum; //维护总和
}tree[4*500010];
int n,m,a[500010];
inline int read(){
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')f=-1;ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=x*10+ch-48;ch=getchar();
    }
    return x*f;
}
void pushup(int p){
    tree[p].sum=tree[p*2].sum+tree[p*2+1].sum;
}
void build(int p,int l,int r){
    tree[p].l=l,tree[p].r=r; //当前树的管理区间范围
    if(l==r){
        tree[p].sum=a[l]; //叶子节点直接赋值
        return;
    }
    int mid=(l+r)/2; //区间中点
    build(p*2,l,mid); //递归建左子树
    build(p*2+1,mid+1,r); //递归建右子树
    pushup(p); //回传sum
}
void update(int p,int x,int k){
    if(tree[p].l==tree[p].r){ //要修改的节点
        tree[p].sum+=k; //直接修改，返回
        return;
    }
    int mid=(tree[p].l+tree[p].r)/2;
    if(x<=mid)update(p*2,x,k); //在左子树，递归到左边
    if(x>mid)update(p*2+1,x,k); //在右子树，递归到右边
    pushup(p); //回传sum
}
long long query(int p,int l,int r){
    if(tree[p].l>=l&&tree[p].r<=r){ //在查询区间内
        return tree[p].sum; //直接返回值
    }
    long long ans=0;
    int mid=(tree[p].l+tree[p].r)/2;
    if(l<=mid)ans+=query(p*2,l,r); //如果左子树区间有重叠部分，答案加上左边的查询
    if(r>mid)ans+=query(p*2+1,l,r); ////如果右子树区间有重叠部分，答案加上右边的查询
    return ans;
}
int main(){
    n=read(),m=read();
    for(int i=1;i<=n;i++){
        a[i]=read();
    }
    build(1,1,n); //从根节点出发，建造 [1,n] 区间的线段树
    while(m--){
        int op,x,y;
        op=read(),x=read(),y=read();
        if(op==1){
            update(1,x,y); //从根节点出发，区间 [x,x] 的值 +y
        }
        else{
            long long ans=0;
            printf("%lld\n",query(1,x,y)); //从根节点出发，查询区间 [x,y] 的总和
        }
    }
    return 0;
}

因为需要操作 $m$ 次，所以整体时间复杂度为 $O(m \log n)$ 。

线段树区间修改

要把线段树的一段区间修改为某个值，最简单、最暴力的方法是遍历每一个节点暴力单点修改。

但是这种方法的时间复杂度是炸的，单次暴力区间修改时间复杂度 $O(n \log n)$ ，$q$ 次修改时间复杂度 $O(q·n \log n)$ ，甚至比直接暴力循环修改的时间复杂度还多一个 $\log$ 。

为什么这样子复杂度这么高呢？我们可以画个图。集合 $\{8,3,11,4,13\}$ ，区间 $[1,3]$ 统一加 $5$ ，要修改到的节点如下图所示：

总之可以看到，画绿线的节点都是修改区间下的子节点，其实完全没有逐一修改的必要。我们可以先让区间节点修改了，再加上一个“懒”标记，查询时再下传到子节点里面，这样可以大幅提升效率。

“懒”标记指的是当前节点修改过了，但没有让下边的节点修改的一种标记，可以再查询时需要时下传，大大节省时间，所以是懒标记。

最后

好了，就暂时先写到这里吧，因为这个蒟蒻要卷whk干其他事，就先咕咕了。

已知错误：

由于这个蒟蒻的知识短浅疏忽，误将树形视图的方括号写成了圆括号，因为太多改不过来了。

请各位大佬帮忙指出文章的问题，以免误人子弟。